Johannes Kepler (1571–1630)
Johannes Kepler was born on December 27, 1571 in Weil der Stadt, near Stuttgart, into a modest family. He graduated from the University of Tuebingen, where he studied mathematics and astronomy under Michael Maestlin (1550-1631), an early supporter of the Copernican system. In 1594, while engaged in the final year of his studies in theology, he was given the chair of mathematics at Graz, where he became increasingly absorbed in astronomy.

Painting of Johannes Kepler.
Wikipedia
Kepler was formally expelled from town in 1600 on account of his open adherence to the Protestant faith. He first came to Prague in 1599 to work as an assistant to Tycho Brahe, and upon Tycho's untimely death in 1601 inherited his massive stock of accurate planetary observations, as well as his job as Imperial Mathematician to Rudolf II. In 1612, following the downfall of Rudolf II he moved to Linz, in 1621 to Ulm, and in 1627 to Sagan.
Through a quarter century of painstaking calculations Kepler brought the Copernican system to its modern form by replacing Copernicus' circular heliocentric orbits by ellipses, with the Sun at one focus. The process through which he arrived at his justly famous Laws of Planetary Motion was often a contorted one, as Kepler's peculiar mixture of physical insight and mystical inclinations lead him to seek causes for the number and arrangement of planetary orbits, as opposed to constructing purely mathematical descriptions. His first such model involved the "nesting of the five regular solids” and was published in his 1596 “Mysterium Cosmographicum." While never relinquishing this idea, in his 1619 "Harmonices Mundi" he also sought an explanation in terms of musical harmonies. Hidden deep in this work is the first statement of Kepler's so-called Third Law, establishing the proportionality of the square of planetary orbital periods to the cube of their mean distance to the Sun.
Kepler's first two Laws of Planetary Motion were first outlined in his 1609 "Astronomia Nova," but laid out in detail together with his Third Law in book IV of his monumental work "Epitoma astronomia Copernicanae", published between 1617 and 1621. The underlying physical explanation of his Laws would have to wait over half a century, until Isaac Newton provided the answer in terms of the theory of universal gravitation.
In 1627 Kepler also finally published what was to be the crowning (but somewhat belated) achievement of Tycho Brahe's career: the "Rudolphine Tables" of planetary positions. These made full use of Tycho's store of accurate observations in conjunction with Kepler's new model for planetary orbits. Because of Kepler's position as Imperial Mathematician, his enthusiastic public endorsement of Galileo Galilei's telescopic discoveries did a lot to promote the latter's fame in northern Europe.
On May 28, 1607 Kepler used his newly devised camera obscura to observe the solar disk and saw a sunspot, which he mistook for a transit of Mercury, to the amazement of later astronomers who all agreed that of all people, Kepler really should have known better.
Kepler was a prolific author by any standards. Besides his astronomical books, he is credited by some with having written the first science fiction novel, his "Somnium," which was published posthumously in 1634 and described a voyage to the Moon. He wrote extensively on geometrical optics, and was the first to correctly sort out once and for all the production of real versus virtual images by mirrors and lenses. He is also said to have laid the foundations of crystallography in a little book on snowflakes written as a New Year's gift to his patron Rudolf II in 1611.
On the move again because of religious persecution, he fell ill, and died on November 15, 1630 in Regensburg.
Bibliography
Caspar, M. 1959, Kepler, [1993 Dover reprint].
Beer, A., & Beer, P. (eds.) 1975, Kepler, vistas in astronomy vol. 18, Pergamon Press.
Gingerich, O. 1989, Johannes Kepler, in The General History of Astronomy, vol. 2A, eds. R. Taton and C. Wilson, Cambridge University Press, pps. 54-78.
Kepler's Observations
Mysterium Cosmographicum
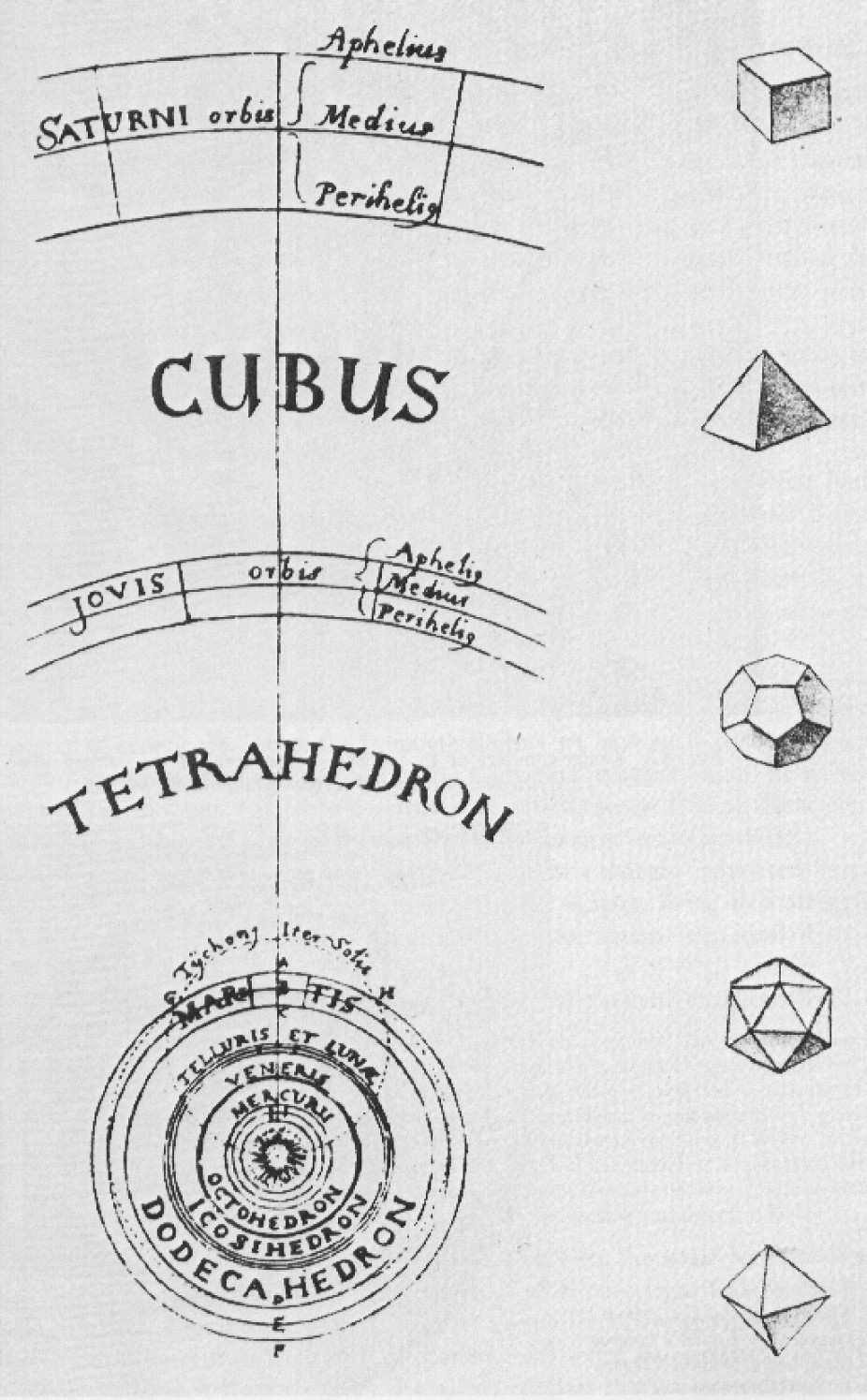
Kepler's sketch shows an ordering of the five planetary orbits in terms of the nesting of the five regular solids.
Published on July 19, 1596, Johannes Kepler's first major astronomical work, "Mysterium Cosmographicum (The Cosmographic Mystery)," was the first published defense of the Copernican system. He hypothesized that regular polygons bound one inscribed and one circumscribed circle at definite ratios, which, he reasoned, might be the geometrical basis of the Universe. Despite rather poor agreement between his model and his observations, Kepler would cling to this idea to the end of his life. He issued a second edition of the book in 1621.
Kepler sought the opinions of many of his astronomical contemporaries to whom he had sent copies of his Mysterium, among them, Tycho Brahe. On February 4, 1600, Kepler met Tycho Brahe and his assistants, in Prague, the site where Tycho's new observatory was being constructed. Over the next two months he stayed as a guest, analyzing some of Tycho's observations of Mars. In August of 1600, Kepler returned to Prague, with his family, to collaborate on the Rudolphine Tables.
New Astronomy

Front page of Kepler's "New Astronomy (Astronomia Nova)."
Kepler's "New Astronomy (Astronomia Nova)" was completed and published in Linz in 1609. Buried deep in this at times very mystical book, is Kepler's first formulation of his first and second Laws of planetary motion, which in modern parlance can be stated as follows:
- Planetary orbits are ellipses, with the Sun located at one focus;
- Planets move along their elliptical orbit with a speed such that a line segment joining the planet to the Sun sweeps equal surface areas in equal time intervals.
Another important novelty is Kepler's attempt to justify the above two laws on physical grounds, by ascribing planetary motions to a form of magnetically-mediated action-at-distance. This insight is what led him to formulate planetary orbits in relation to the Sun, as opposed to the center of the Earth's orbit (or "mean sun"), and in turn to his first two laws. This idea, interestingly, also led him to propose that the Sun rotates on its axis, two years before telescopic observations of sunspots would establish solar rotation as a fact.
The Rudolphine Tables

Frontispiece of Kepler's "Rudolphine Tables" of planetary positions.
The "Rudolphine Tables" was published by Kepler in 1627 in Ulm and dedicated to Tycho's and Kepler's deceased patron, Emperor Rudolph II. The frontispiece is an allegoric depiction of the Temple of Astronomy. Nicolaus Copernicus and Tycho Brahe take center stage, while Hipparchus and Claudius Ptolemy look on. The central panel on the base is a map of the island of Hveen. The panel to the left shows Kepler, himself, laboring by candlelight.
The "Rudolphine Tables" were the first to make use of Kepler's newly formulated "Laws on Planetary Motions", calibrated using Tycho's store of accurate planetary observations. They received a spectacular validation on November 7, 1631, when the French philosopher and sometimes astronomer Pierre Gassendi (1592–1655) observed a transit of Mercury across the solar disk, as predicted by Kepler. Kepler's prediction of this event was far more accurate than those based on the Copernican Tables. This success paved the way for the general acceptance, not only of the Rudolphine Tables, but also, by extension, of Kepler's three lLaws of planetary motions.
Harmonices Mundi

Front page of Kepler's "Harmony of the World (Harmonices Mundi)."
Kepler's "Harmony of the World (Harmonices Mundi)" was completed in the spring of 1618 and finally published in Linz in 1619. Again of a rather mystical flavor at times, the book contains Kepler's first formulation of his third law of planetary motion: "The square of a planet's orbital periods is proportional to the cube of its mean distance to the Sun."
Kepler was to formulate the final versions of his three laws of planetary motions much more clearly in book IV of his textbook "Epitome of Copernican Astronomy (Epitome Astronomiae Copernicanae)," published in 1620.
Epitome of Copernican Astronomy

Page from Kepler's "Epitome of Copernican Astronomy (Epitome astronomiae Copernicanae)"
Kepler's "Epitome of Copernican Astronomy (Epitome astronomiae Copernicanae)", was one of his most ambitious and life long projects, second perhaps only to his "Rudolphine Tables." Books I through III, appeared in 1618, Book IV in 1620, and Books V-VII in 1621. The complete work was reprinted in 1635, and for a long time remained one of the few comprehensive textbooks on the topic. Kepler applies his third law of planetary motion to infer the sizes of the orbits of the Galilean moons of Jupiter.
Bibliography
Kepler, J. 1609, Astronomia Nova, trans. W.H. Donahue 1992, Cambridge University Press.
Stephenson, B. 1994, The Music of the Heavens, Princeton University Press.
Stephenson, B. 1987, Kepler's physical astronomy, [1994 reprint, Princeton University Press].