The Sun as a Dynamo
The ultimate origins of solar variability lie below the visible surface, where turbulent convection, differential rotation, and meridional flows work together to produce magnetic fields through the operation of a stellar dynamo, giving rise to the 22-year solar magnetic cycle.
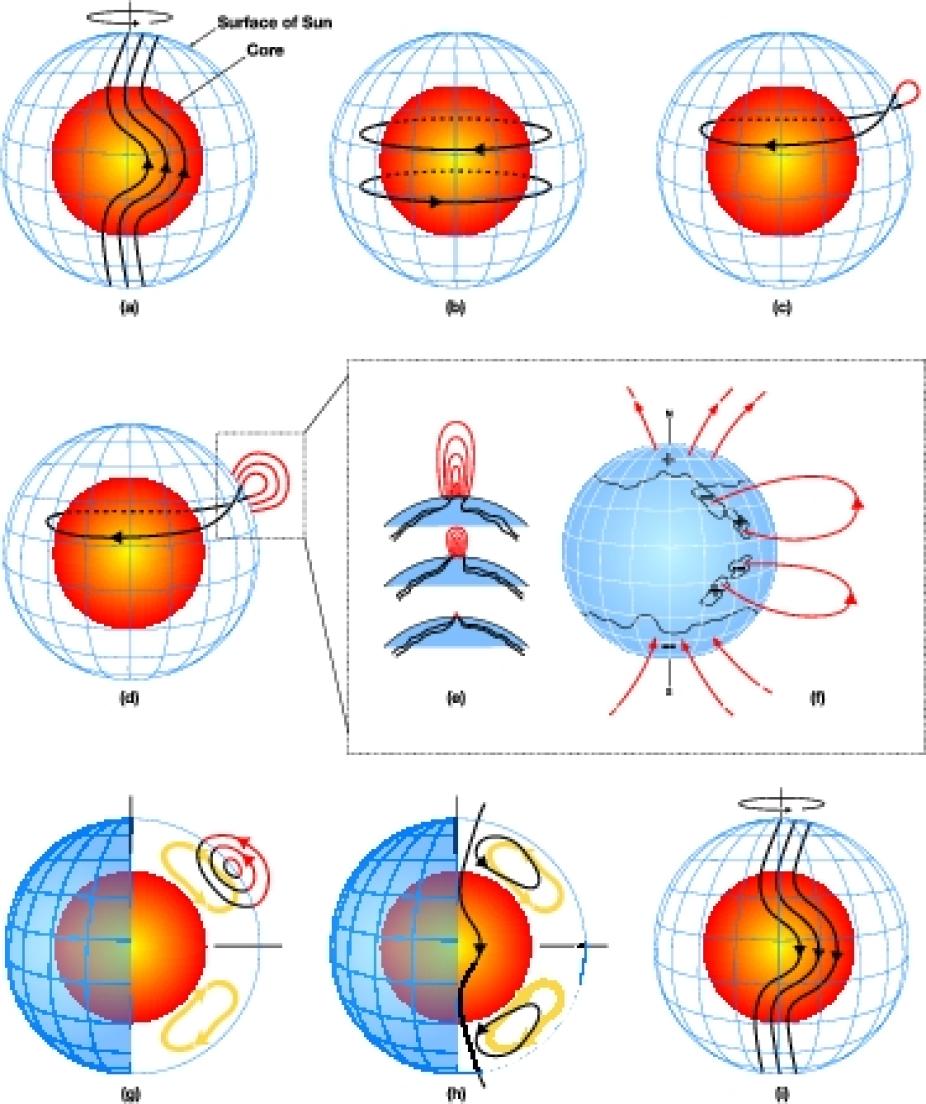
Figure 1: Schematic of solar flux-transport dynamo processes. Red inner sphere represents the Sun's radiative core and blue mesh the solar surface. In between is solar convection zone where dynamo resides. (a) Shearing of poloidal field by the Sun's differential rotation near convection zone bottom. The Sun rotates faster at the equator than the pole. (b) Toroidal field produced due to this shearing by differential rotation. (c) When toroidal field is strong enough, buoyant loops rise to the surface, twisting as they rise due to rotational influence. Sunspots (two black dots) are formed from these loops. (d,e,f) Additional flux emerges (d,e) and spreads (f) in latitude and longitude from decaying spots. (g) Meridional flow (yellow circulation with arrows) carries surface magnetic flux poleward, causing polar fields to reverse. (h) Some of this flux is then transported downward to the bottom and towards the equator. These poloidal fields have sign opposite to those at the beginning of the sequence, in frame (a). (i) This reversed poloidal flux is then sheared again near the bottom by the differential rotation to produce the new toroidal field opposite in sign to that shown in (b).
To seek the theoretical explanation of the cyclic evolution of the solar magnetic features, in the past an oscillatory dynamo in the Sun was postulated. Nowadays it is widely accepted that a magnetohydrodynamic dynamo is indeed responsible for generating and maintaining the magnetic fields of the Sun in the solar convection zone and neighboring layers. This means that the fluid flow of highly conducting plasma there maintains electric currents and (by Amperes law) associated magnetic fields against ohmic dissipation. The history of dynamo theory applied to the sun goes back more than 50 years, to pioneering papers of Eugene Parker.
Solar dynamo research at the High Altitude Observatory started in the 1970s with the work of two visiting scientists, Michael Stix and Hirokazu Yoshimura, using large-scale, kinematic, mean-field models, whereas the more detailed full 3D MHD models were built in the 1980s (Gilman 1983). Almost nothing was known about the solar interior properties at that time. With the advent of helioseismology in late 1980s, the solar dynamo theory has significantly evolved. In the 1990s, two streams of dynamo research developed at HAO. One was the 'interface' dynamos (MacGregor & Charbonneau 1997) and the other was the “flux transport” dynamos (Dikpati & Charbonneau 1999). To date flux-transport dynamos have been the most successful at reproducing and explaining the main features of a solar magnetic cycle. Over the past decade, HAO has been one of the leaders in research on this class of dynamo. The basic workings of a flux-transport dynamo applied to the sun are demonstrated in the schematic diagram (Figure 1).
2D Flux-transport dynamos for the sun
Over the past decade, in the course of developing and exploring the details of 2D flux-transport dynamo, recently a flux-transport dynamo-based predictive tool has also been developed at HAO (Dikpati, de Toma & Gilman 2006) to simulate and predict solar cycle properties.
Observations indicate the existence of time-variations in differential rotation, in the form of torsional oscillations, which correlate well with with the butterfly diagram. Therefore in dynamo models it is necessary to include feedbacks of magnetic fields on the flow fields that produce the magnetic induction. So modeling a dynamical dynamo has been another area of HAO's dynamo research (Rempel 2006).
So far, flux-transport dynamos have been built to be axisymmetric about the solar rotation axis, and can explain well the longitude-averaged solar cycle features. However, observations indicate the existence of longitude-dependent solar cycle features also. So currently a major research effort at HAO is to generalize dynamos to 3D, using two different approaches with similar goals: one includes large-scale non-axisymmetry through low longitudinal wavenumbers in the flow and magnetic fields; the other is a full 3D MHD approach (Miesch et al. 2008).
While solar cycle research is an intriguing and actively ongoing effort, one scientist observes only one or two full magnetic cycle their entire research career. Therefore to understand solar cycle, it is necessary to study stellar dynamos including particularly stellar magnetic activity, another active research area at HAO (Metcalfe et al. 2007).

In axisymmetric flux-transport dynamo models the magnetic fields simulated include the longitudinal or toroidal field, and the field in meridional planes, or poloidal field. A typical evolution of large-scale toroidal and poloidal fields in the Sun are displayed in the animation movie.
The line-contours represent the poloidal fields in the plane of the screen and the color-shades the toroidal field perpendicular to the screen. Poloidal fields are generated by the Babcock-Leighton effect at the surface; then they migrate poleward by the surface meridional flow and cause polar field reversal. A remnant component of these poloidal fields is transported down to the bottom of the convection zone by the downward flow at high-latitudes, and starts getting sheared by the Sun's differential rotation to induce the spot-producing toroidal fields. The emergence of 'tilted' patterns of magnetic flux at the surface that originates from toroidal fields near the bottom of the convection zone, creates the source for new cycle's poloidal fields. However, the flux emergence process has so far been captured in a parameterized form for simplicity. The turbulent diffusion of magnetic flux works everywhere at all times.
Flux-transport models have now provided plausible explanations for the following:
- The cycle period, which is determined in such models primarily by the speed of the meridional flow at the bottom of the convection zone (Dikpati & Charbonneau 1999). The equatorward flow speed there is not known directly from observations; it is determined from the observed surface flow-speed and applying the constraint of mass conservation.
- The near-coincidence in time between the epoch of sunspots' peak and the epoch of polar field reversals, which is governed by the poleward surface meridional flow and the supergranular type diffusion there.
- The dominant symmetry of the solar magnetic field about the equator (radial field antisymmetric or 'dipole' like) (Dikpati & Gilman 2001). The inclusion of tachocline alpha-effect in the model, a process of lifting and twisting of toroidal fields at the base of the convection zone, arising from MHD instabilities very likely occurring there, favors the correct symmetry.
- Differences in polar field reversal characteristics between North and South poles in a particular cycle (such as relative timing), namely cycle 23 (Dikpati et al. 2004). These are caused by a combination of differences in surface poloidal sources and differences in meridional flow speeds and patterns in North and South hemispheres.
The robustness of flux-transport dynamo models has been demonstrated with a set of 'benchmark' tests on eight different dynamo codes, including two from HAO, that use widely differing numerical schemes but get virtually the same results for the simulation of an alpha-omega convection zone dynamo and a Babcock-Leighton dynamo. (Jouve et al. 2008).
Application to solar cycle prediction
Attempts have been made for at least the past 40 years to predict the strength of the next solar cycle. Accurate predictions of the peak amplitude and its timing have great practical as well as scientific value. Strong solar cycles can negatively impact many industries, such as power transmission and satellite communications. Strong cycles expand the upper atmosphere, increasing the drag on all orbiting satellites.
Historically, solar cycle predictions have been based on statistical methods, extrapolating from past behavior of the sun. Different methods have produced widely varying forecasts for the same cycle. By contrast, enormous progress has been made in the past 60 years in skillfully predicting future weather and climate by use of numerical models that integrate forward in time the governing laws of physics. Predictive research of this type for the solar cycle started only in the past five years, first in HAO, in the form of integrating forward in time the flux-transport dynamo equations assimilating data of the Sun's past magnetic field.
Necessary conditions for building a predictive solar cycle model that can assimilate date and show good skill in such predictions are that (i) the model must be as constrained as possible by observations, (ii) the model must be calibrated to an average solar cycle, (iii) the model runs must start with reliable initial conditions and continuous assimilation of observed data. Just as ENSO predictions for the Earth's coupled ocean-atmosphere system require a memory of past ocean surface temperatures, in order to have predictive skill for future cycles the Sun and the dynamo model both need to have some memory of past solar magnetic fields. Due to meridional circulation, some memory of the past few cycles' magnetic fields is an inherent characteristic of a flux-transport dynamo model. In particular, for the observed poleward meridional flow at the surface, and with an equatorward return-flow at the base of the convection zone, constructed from mass conservation, dynamo simulations indicated that the poloidal magnetic flux at the surface takes 17-22 years to be 'recycled' or transported via the meridional circulation conveyor belt from the high-latitudes at the top to the mid-latitudes at the bottom of the convection zone. Thus in a flux-transport dynamo model, the 'seed' for a future cycle is formed at the base of the convection zone, from the combination of of the recycled poloidal flux of past cycles. This gives the model the potential for predicting the strength of a new cycle. This hypothesis has been explored (Dikpati, de Toma & Gilman 2006) by integrating forward in time the flux transport dynamo equations, driven by continuous input of observed magnetic data at the upper surface. Meridional circulation also contributes to good calibration of a large-scale mean-field dynamo, no matter whether the dynamo is driven by an interface or Babcock-Leighton alpha-effect (Dikpati, Gilman & MacGregor 2005).
The surface poloidal magnetic field source is critical to making predictions with a flux-transport dynamo calibrated to the sun. This source should be derived from the observed poloidal flux estimated from the decay of active regions. Surface magnetic fields have been measured only over the past three solar cycles, but sunspot areas are known reliably for the past twelve. The spot-area correlates strongly with surface magnetic flux (Figure 2). Thus it is possible to use the much longer sunspot area record as a proxy for surface magnetic fields and its time-variation is captured in a simplified way by a migrating Gaussian (Figure 3).
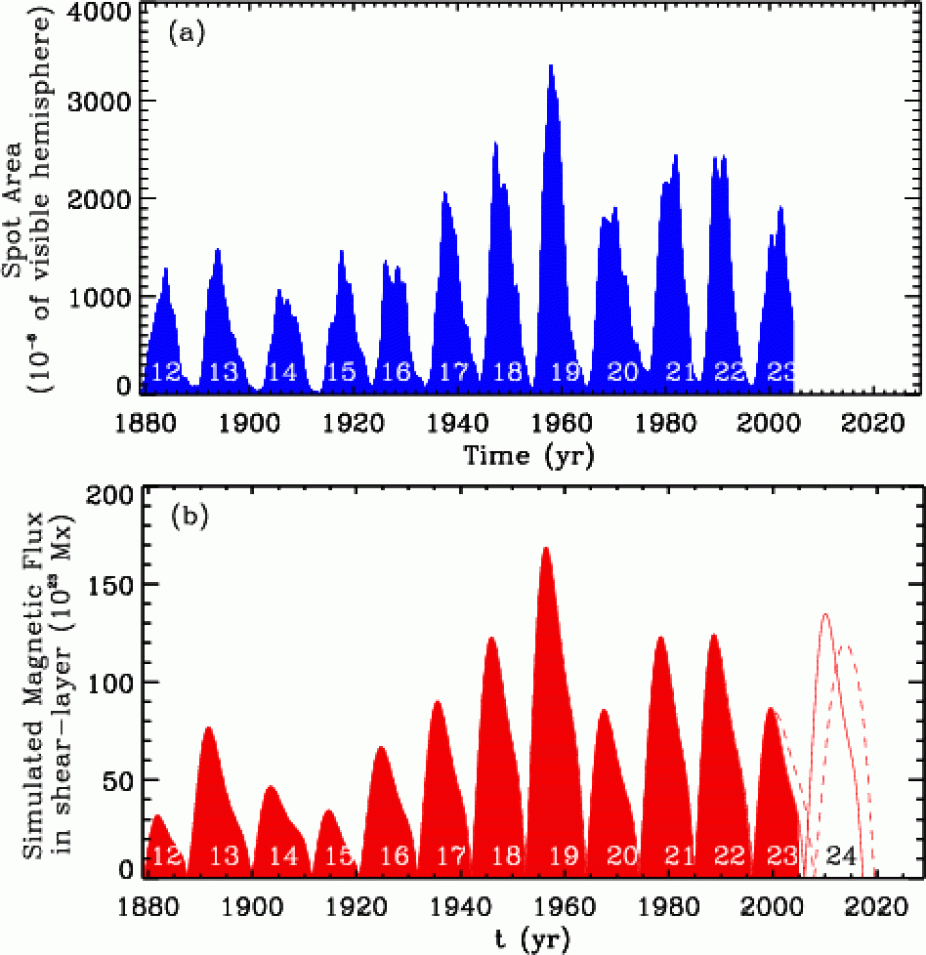
Figure 2: Spot-area correlates strongly with surface magnetic flux.
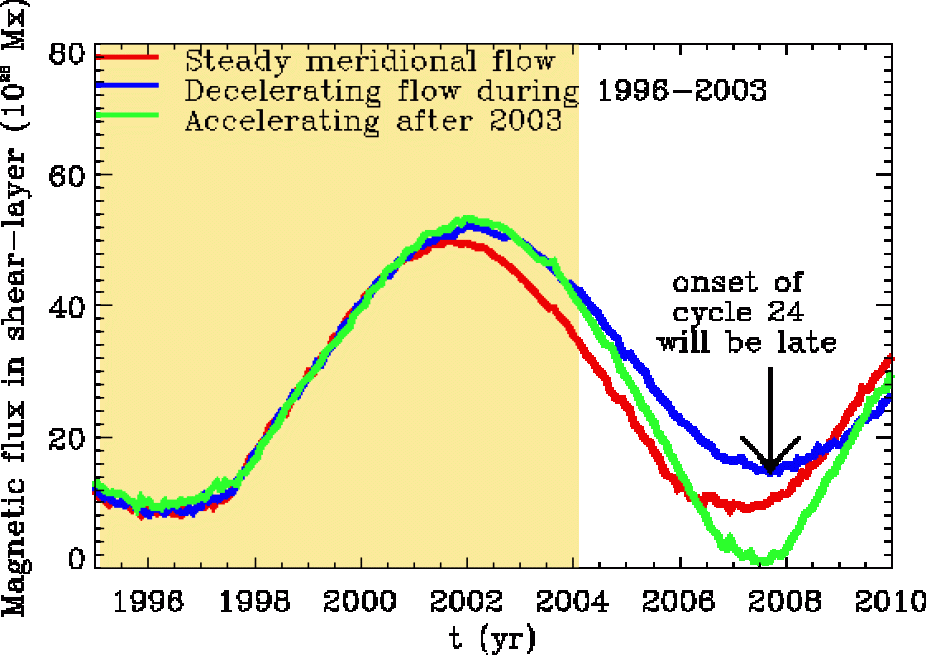
Figure 3: Migrating Gaussian plot of magnetic flux.
Several forecasts of solar cycle features for the upcoming cycle 24 such as the onset-timing, amplitude, north-south asymmetry have been made as a part of HAO's dynamo research. By now the delayed onset of cycle 24 predicted at HAO has been verified within the error-bar set by the mean-field approximations, while the other predictions about the cycle 24 features are yet to be verified. Currently HAO's on-going effort on solar cycle prediction research is to develop a more sophisticated 'sequential' data-assimilation scheme, in collaboration with IMAGe scientists.
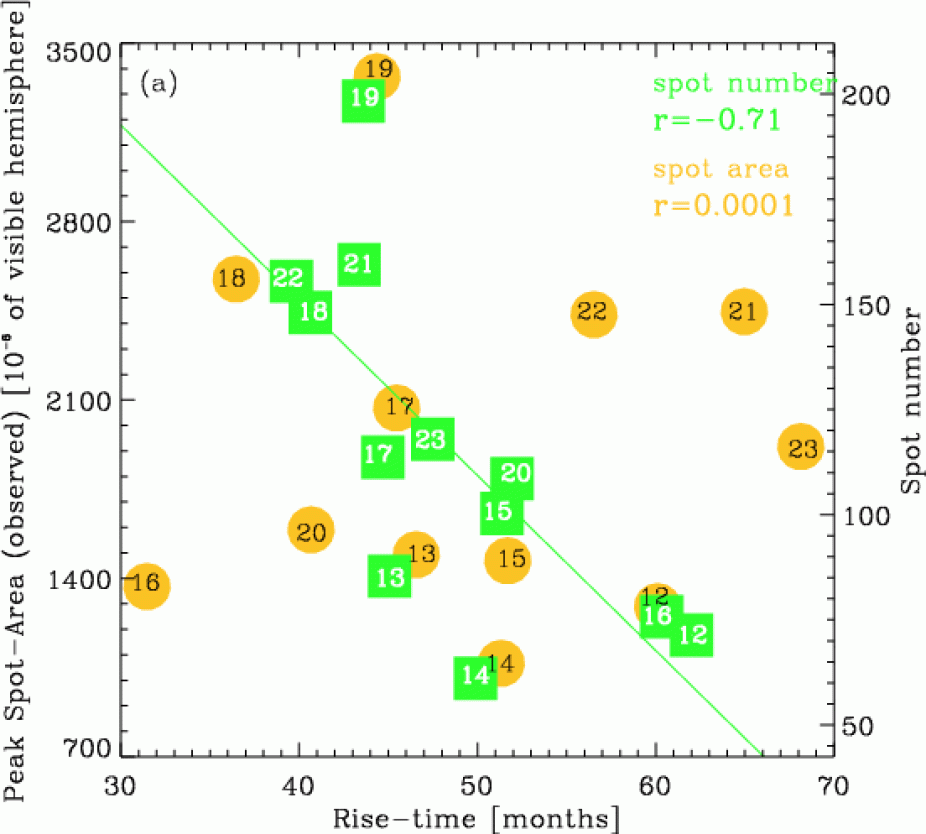
Figure 4: Yellow circles show scatter plot of correlations between observed peak spot area and cycle rise time; green squares show that between Zurich sunspot number peak and cycle rise time.
In order to determine whether the origin of the high skill in amplitude prediction is due to an inherent Waldmeier effect introduced into the model through the migrating Gaussian surface poloidal source derived from spot-area data, the (non)existence of this effect in sunspot-area data was established. The Waldmeier effect is the anti-correlation between the rise-time of a cycle and the peak number of sunspots in that cycle. Surprisingly the Waldmeier effect is an artifact of the Wolf sunspot number (Dikpati, Gilman & de Toma 2008), but is not present in any other proxy for the solar cycle, such as spot area, group spot number, f10.7 flux (Figure 4).
2D Dynamical dynamo
In a 2D kinematic regime, the mean-field induction equation is solved, subject to the constraint that the magnetic field is divergence-free. The velocity fields used in the induction equation are prescribed. However, in reality magnetic fields can react back on the fluid motions. For flux-transport dynamos, therefore, both the differential rotation and the meridional circulation may be dynamically modified. Such back-reactions have been studied (Rempel 2006) using a non-kinematic version of a flux-transport dynamo.
There is observational evidence on the sun of such feedbacks, called torsional oscillations. These are observed perturbations on the time-averaged differential rotation of the sun, originally discovered by Robert Howard and Barry LaBonte of the Carnegie Observatories, using solar surface velocity data collected at Mt Wilson. Since their original discovery, more refined observations of surface doppler motions as well as helioseismic measurements have resulted in the current picture. The perturbations of faster and slower than average rotation speeds (full range ~10 m/sec) are linked in phase to the solar cycle. There is an equatorward migrating branch in middle and low latitudes, and an even stronger poleward migrating branch at high latitudes. There appears to be significant amplitude in the torsional oscillations throughout the solar convection zone, as detected helioseismically.
The amplitude of these torsional oscillations compared to the average differential rotation is no more than about 5%. This relatively small amplitude therefore puts an upper limit on the strength of magnetic fields induced. Still stronger fields would cause still larger perturbations in the differential rotation. This puts a constraint on all dynamo models to limit the size of induced fields to a level consistent with the observed velocity variations through a solar cycle.
Even though the meridional circulation is relatively weak compared to differential rotation, it gets modified significantly only where the induced toroidal field is extremely strong, well above equipartition of kinetic and magnetic energy. This is because the meridional circulation results from a slight imbalance of very large forces, so the work that can be done can greatly exceed the kinetic energy of meridional circulation. By contrast, the differential rotation is more easily damped by the feedbacks.
This non-kinematic model has further shown that both the poleward and equatorward branches of the torsional oscillations can be explained by electromagnetic effects. The poleward branch is a consequence of jxB forces altering the differential rotation, while the equatorward branch is produced indirectly, by the electromagnetic forces changing the thermal structure of the convection zone.
Such back-reaction could also extend even to turbulent part of the flow fields 'quenching' the turbulent magnetic diffusivity, because the electromagnetic body force could alter the form of the turbulence. Thus there may be both macroscopic and microscopic effects to consider, however the subject is relatively less explored compared to alpha-quenching. A recent work (Guerrero, Dikpati & Dal Pino 2009 has shown that the diffusivity-quenching helps amplify the toroidal field strength up to a value required by the rising flux tube simulations and lengthen the dynamo cycle.
Full 3D MHD simulations
Three-dimensional MHD simulations provide further insight into how organized magnetic activity patterns can arise through the combined action of turbulent convection, differential rotation, and meridional circulation (read more »). Turbulent dynamos often tend to build turbulent, small-scale magnetic fields but rotation and stratification impart helicity (both kinetic and magnetic) to solar convection that promotes the generation of larger-scale flux structures. Rotational shear also plays an essential role, stretching and amplifying fields into ribbons and sheets of toroidal flux (see figure). This is particularly efficient in the solar tachocline, which is thought to act as a factory and repository for the generation and storage of toroidal magnetic flux. MHD simulations of penetrative solar convection exhibit downward pumping of magnetic flux into the tachocline where it is amplified and organized by rotational shear (Figure 5 & 6).
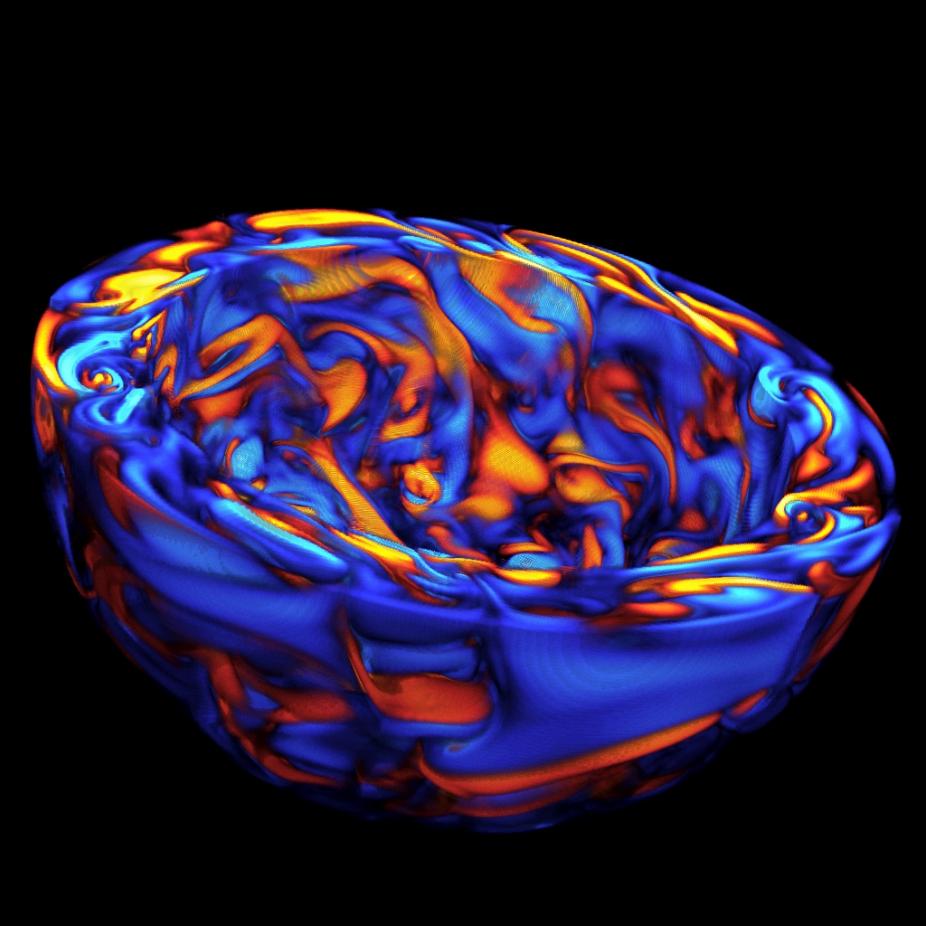
Figure 5: Volume visualization of the longitudinal magnetic field component in a 3D MHD simulation of solar convection. Blue and red denote eastward and westward flux respectively and the northern hemisphere is removed in order to highlight the structure in the equatorial plane. Rotational shear stretches fields into toroidal ribbons and sheets while vortical convective downflows penetrate through, cleaving and wrapping the ribbons and recycling the flux.
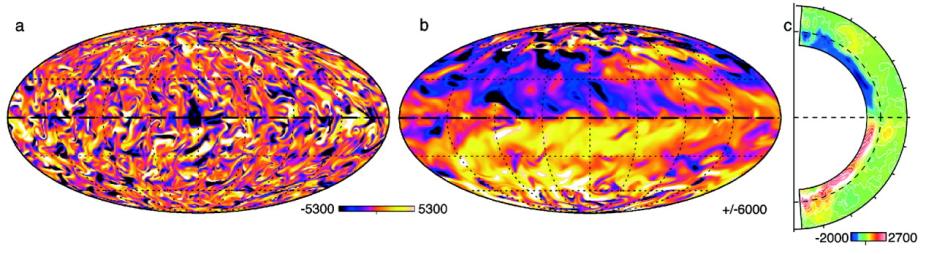
Figure 6: Pumping, amplification, and organization of toroial magnetic fields in a global MHD simulation of solar convection that incorporates a stably-stratified tachocline of rotational shear below the base of the convection zone. Panels a and b illustrate the longitudinal magnetic field component in the mid convection zone and in the tachocline respectively, each in a Molleweide projection. Red and blue represent eastward and westward field as indicated in the color bar. The field in the convection zone is dominated by turbulent fluctuations while the tachocline field is more ordered, with prominent sheets of toroidal flux that are antisymmetric about the equator. This is particularly apparent in the longitudinally averaged toroidal field shown in frame c. [Miesch et al].
Stellar Dynamos
The solar/stellar connection is another active area of HAO's dynamo research. It is very likely that all stars with either convection zones or convective cores have such dynamos, though for different stellar parameters, such as rotation, the form the dynamo takes may be very different. And stars with convective cores are likely to have distinctly different dynamos than stars with convective envelopes. It is well known from observations that many stars with convective envelopes as thick as or thicker than that of the sun are also cyclic, with dynamo periods ranging from a few years to a few tens of years. The differential rotation of some of these stars is known from observations, but the meridional circulation is not. Therefore stellar dynamo research is a vast area with many topics being pursued simultaneously.
In the case of stars with convective cores, such as early-type stars, the top surface of the dynamo can not be observed because it is hidden inside a radiative envelope. But these stars do show substantial surface magnetic fields. The time-dependence these fields show is readily explained by the so-called oblique rotator model, which assumes a dipole-type field is present, whose axis is tilted compared to the rotation axis. But what is the origin of this surface field? A dynamo origin for this field has been extensively examined (MacGregor 2005). Such fields can be produced by dynamo action from the interaction of convection with the core rotation, if there is only small rotation present. Dynamos of the so-called "alpha^2' type produce fields that are not 'symmetrized' about the rotation axis. With much more differential rotation present, they become symmetrized and will produce a surface field of a different type, not in as close agreement with observations.
Another problem is how the dynamo fields in the core get to the surface to be observed. One candidate is meridional circulation. Charbonneau and MacGregor (ApJ 559,1094,2001) showed that a meridional circulation large enough to transport the fields to the surface is also large enough to interfere with the internal workings of the dynamo, effectively quenching dynamo action altogether. A promising alternative mechanism is the formation of buoyant flux tubes in the core, which then are sufficiently magnetically buoyant to rise throught the stably stratified envelope to the surface. (MacGregor & Cassinelli 2003). showed that this hypothesis is theoretically plausible, with tube taking 10^3-10^4 years to reach the surface.
A solar-type flux-transport dynamo model has been used to seek the origin of long-term non-reversing fields in solar/stellar interior (Dikpati, Gilman & MacGregor 2006). While the mechanism of skin-depth limits the penetration of the dynamo-generated oscillatory fields down to only a few kilometers below the base of the convection zone (the domain where the dynamo operates), the penetration of the non-reversing component down through the radiative core is determined by diffusive leaking. There could be preference in the sign of such non-reversing magnetic field in the radiative solar/stellar interior, decided by the overlying dynamo; however the field could exist for a million of years. Such a time-scale is very long compared to a dynamo cycle, and hence the non-reversing fields should be observable during some fraction of the entire life of a star.
Solar-Stellar Connection
Just as helioseismology revolutionized our understanding of the interior structure of the Sun, asteroseismology is now placing this knowledge into a broader context, by providing structural information for other solar-type stars. Scientists at HAO are developing a stellar model-fitting pipeline, using a parallel genetic algorithm, to prepare for the asteroseismic data soon expected from several satellite missions. Meanwhile, the Solar Oscillations Network Group (SONG) is a concept for a global network of small ground-based telescopes dedicated to asteroseismology and extrasolar planet searches, currently being organized though the Danish AsteroSeismology Center (DASC) at the University of Aarhus. The High Altitude Observatory is participating in the design and development phase of the SONG effort, with the intent to build and operate one of the SONG telescopes at HAO's Mauna Loa Observatory (MLSO) in Hawaii.
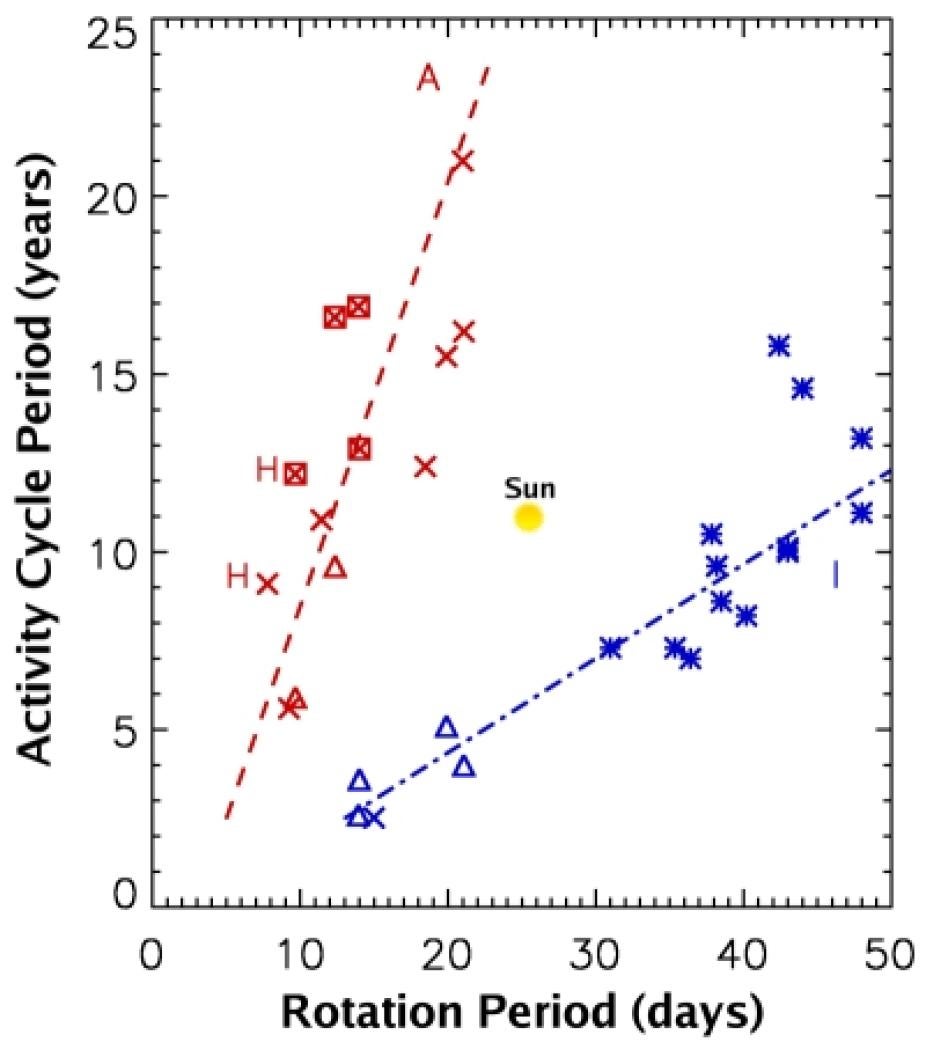
Figure 7: Periods of stellar activity cycles in years, plotted as a function of rotation periods in days. The data follow two sequences: a relatively young, active A sequence (red dashed line) and an older less active I sequence (blue dash-dotted line). The letter H indicates Hyades group stars, crosses indicate stars on the A sequence, and asterisks indicate stars on the I sequence. Squares around the crosses show stars with B-V
Effects associated with rotation can modify stellar properties, altering the luminosities, surface temperatures, sizes, and shapes of stars in ways that are unaccounted for in nonrotating models. HAO scientists have developed methods for constructing self-consistent models of differentially rotating, chemically homogeneous stars, whereby the equations of stellar structure and Poisson's equation for the gravitational potential are iteratively solved for an assumed conservative internal rotation law. Such models provide the means of interpreting observations of stars that are known to be rapid rotators.
If the Sun is peculiar in some way, or if we have fine-tuned our models to reproduce its unique properties, we will never know without studying other stars and attempting to match the diverse observations with the same models. For this reason, HAO is committed to maintaining a connection to stellar astrophysics. By observing magnetic activity cycles in other stars (Figure 7), we can improve our understanding of the solar cycle. By measuring the interior properties of different stars that result in a variety of stellar dynamos, we can place our knowledge of the solar dynamo into a broader context. By modeling the effects of rapid rotation on stellar structure, we can learn about the forces that shaped our own star in the past. Our models must be able to reproduce the wide array of behaviors observed in stars at every stage of their evolution, or their validation must be considered incomplete.
Asteroseismology and Stellar Interiors
Significant progress in dynamo modeling could only occur after helioseismology provided meaningful constraints on the Sun's interior structure and dynamics (Brown et al. 1989; Schou et al. 1998). Later observations, with the capability of detecting helioseismic signatures of solar cycle effects, established that variations in the mean strength of the solar magnetic field lead to significant shifts (~0.5 μHz) in the frequencies of even the lowest-degree p-modes (Libbrecht & Woodard 1990; Salabert et al. 2004). These shifts can provide independent constraints on the physical mechanisms that drive the solar dynamo, through their influence on the outer boundary condition for the pulsation modes. They are thought to arise either from changes in the near-surface propagation speed due to a direct magnetic perturbation (Goldreich et al. 1991), or from a slight decrease in the radial component of the turbulent velocity in the outer layers and the associated changes in temperature (Dziembowski & Goode 2004, 2005).
Space-based asteroseismology missions, such as MOST (Walker et al. 2003), COROT (Baglin et al. 2006), and Kepler (Borucki et al. 2007) are now providing additional tests of dynamo models using other solar-type stars (see Chaplin et al. 2007). The continuous long-term monitoring from these satellite missions and from future ground-based networks like the Stellar Oscillations Network Group (SONG) are expected to yield the precision necessary for asteroseismic measurements of stellar convection zone depths (Monteiro et al. 2000; Verner, Chaplin & Elsworth 2006). By combining such observations with measurements of stellar differential rotation (see below) and the magnetic activity cycles documented from long-term surveys of the Ca II H and K emission (Figure 8), we can extend the calibration of dynamo models from the solar case to many independent sets of physical conditions.
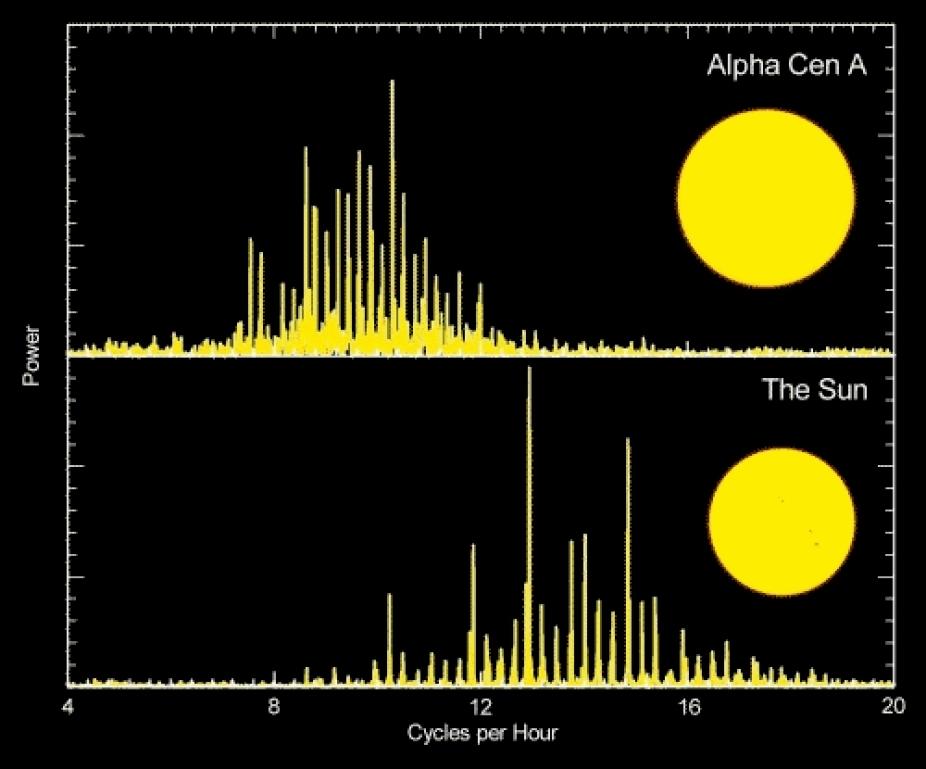
Figure 8: Turbulent convection near the surface of the Sun and other stars excites acoustic oscillations that can be observed from the resulting surface motions and brightness variations. The characteristics of these oscillations probe both the global properties and the interior conditions of the star.
Scientists at HAO are directly involved in the analysis of asteroseismic data from NASA's Kepler mission, including the development of an innovative stellar model-fitting pipeline using a parallel genetic algorithm. As part of an international collaboration known as the Kepler Asteroseismic Science Consortium (KASC), which is being organized through the University of Aarhus in Denmark, HAO scientists have early access to the Kepler data and are characterizing the properties of thousands of solar-type stars (Figure 9). A small sample of the brightest Kepler targets are also being monitored for Ca II H and K emission throughout the lifetime of the mission from the Nordic Optical Telescope in La Palma, Spain.
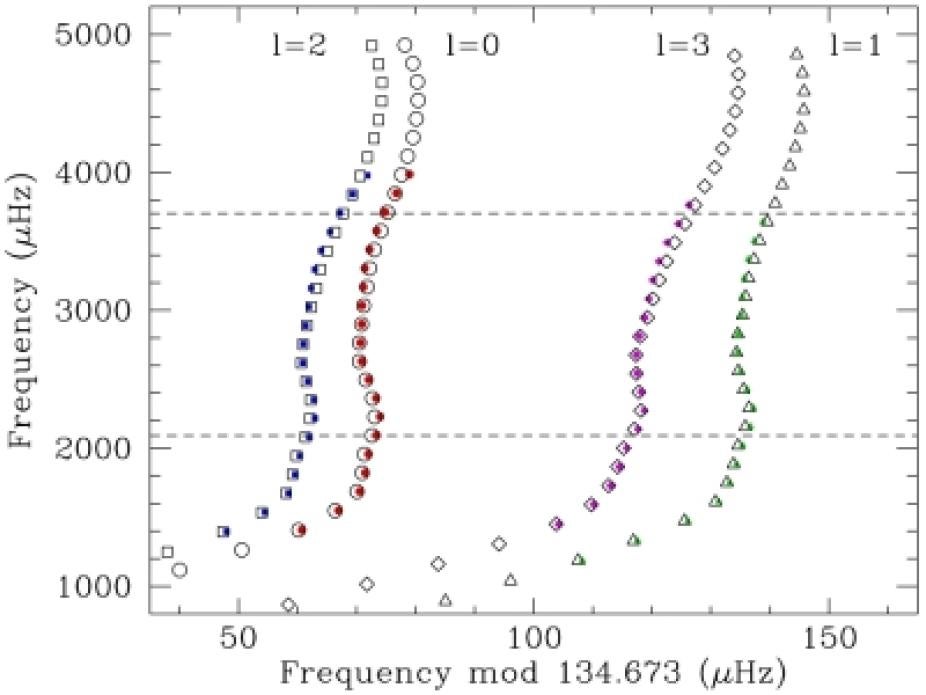
Figure 9: An echelle diagram for the Sun observed as a star, where we divide the oscillation spectrum into segments of a fixed length and plot them against the oscillation frequency. Colored symbols show the observations while open points show the best stellar model from the automated pipeline of Metcalfe et al. (2009). Only the points with l=0-2 between the dashed lines were used for the fit, but the model also provides a good match to the data outside this frequency range and the l=3 points.