RAS Techniques and Instruments: The importance of measuring topological quantities, such as magnetic helicity, in solar observations has long been recognized. In particular, topological quantities play an important role in both understanding and predicting solar eruptions. In this paper, we present ARTop (Active Region Topology), a package that allows researchers to calculate the fluxes of topological quantities based on solar magnetograms. In addition to this, ARTop also allows for the efficient analysis of these quantities in both two-dimensional maps and time series. ARTop calculates the fluxes of magnetic helicity and magnetic winding, together with particular decompositions of these quantities. SHARP magnetograms are downloaded and velocity maps are created using the DAVE4VM method. These data are then used to determine the topological quantities. Analysis tools are included for the straightforward creation of maps and time series for any of the output variables, as well as other functions that are designed to aid solar flare investigations. This code offers researchers a powerful tool for investigating the behavior of active regions and the origins of space weather.
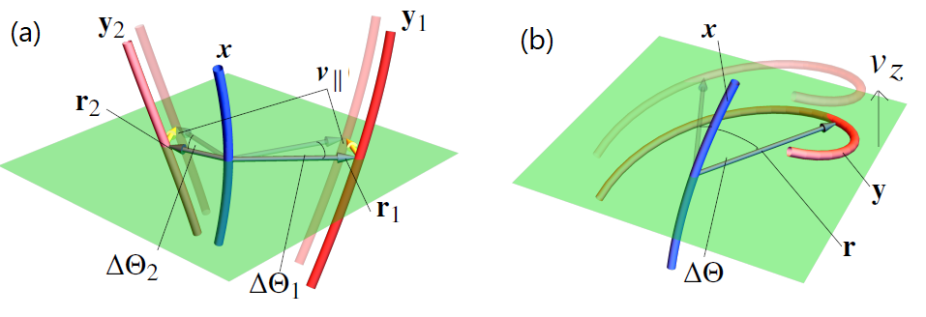
Field line winding due to (a) braiding on the photosphere and (b) emergence through the photosphere. In panel (a) the blue field line x intersects the
photospheric plane, two other field lines y1, y2 also pierce the plane. The vectors r1 and r2 join the intersection points of their field lines and x. The in-plane
fluid velocity 𝒗∥ (shown as yellow arrows) indicates a motion of the field lines y1, y2 due to being “stirred” or “braided” by the plasma (under ideal motion).
This motion leads to the vectors r1 and r2 subtending changes in angle ΔΘ1 and ΔΘ2 with respect to x. The winding measures this rotation and we refer to the
change due to this in-plane motion as braiding motion. In panel (b) we see a helical field line y rising up through the photosphere (at velocity 𝑣𝑧), the kinked
shape means there is apparent foot-point motion and rotation between the curve x and y which can also be tracked by the variation in the change ΔΘ in angle
Θ(x, y) subtended by the two curves. We refer to this motion as emergence motion (which also includes submergence).