MNRAS— (Published: 05 November 2024) Physics of MHD Rossby waves in the tachocline-layer were studied by Dikpati, Gilman, Chatterjee et al. (2020) using a fluid-particle-trajectory approach along with solving vorticity and induction equations. By extending the 2020 MHD Rossby wave model to include a hydrodynamic turbulent convection zone (CZ), they were able to examine how MHD Rossby waves generated in the tachocline might diffuse upward through the CZ to the solar surface. Major findings from this current study include (i) pure hydrodynamic Rossby wave amplitudes decline with height due to viscous diffusion at a rate that is independent of viscosity and increases with longitude wavenumber, (ii) fast MHD Rossby waves amplitude declines faster with height for increasing toroidal field, due to their longitude-phase shifting with height, which increases dissipation of kinetic energy in the wave velocities, (iii) slow MHD Rossby waves decline even faster with height because their longitude-phase shifts more rapidly with height, due to their slow phase speed. Furthermore, it was also found that low wavenumber HD and fast MHD Rossby waves, originating in the tachocline, might be detected at the photosphere, but slow MHD Rossby waves should be virtually impossible to detect. An inference from fluid particle trajectories that wave amplitudes declining with height and longitude phase shifting with height associated with decline, implies a powerful mechanism for tangling of magnetic fields, distinct from convective turbulence effects.
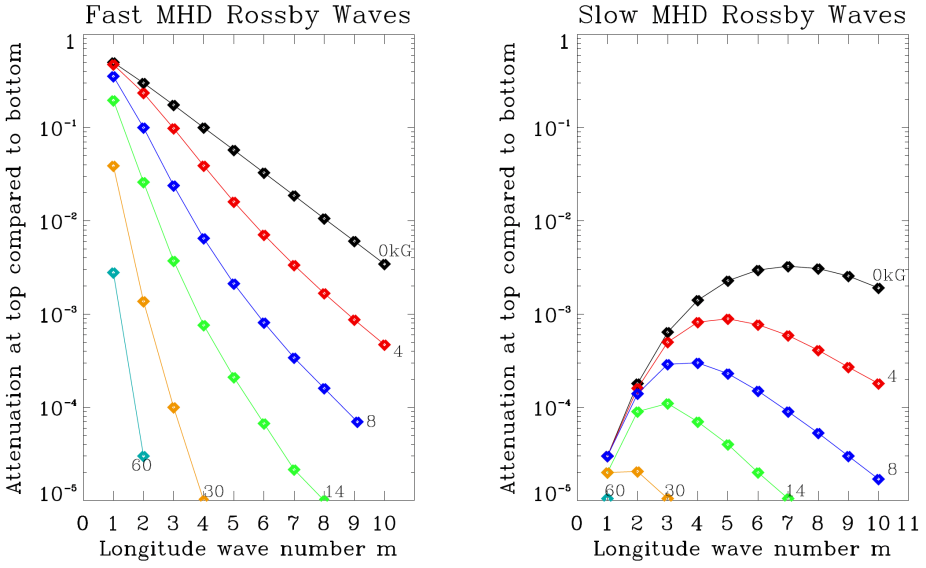
Amplitude decline with height of fast and slow MHD Rossby waves at the top of the channel, centered at 45 degrees latitude, compared to the bottom as a function of toroidal field strength, in kiloGauss, for longitudinal wave numbers m = 1 − 10. Left frame: fast waves; right frame: slow waves. Waves for which amplitude at top is smaller than 10−5 compared to the bottom are not plotted. Amplitude decline with height of the zero kG slow wave is included as a limiting case, even though it does not actually exist in that limit. In the limit of zero toroidal field, the fast wave becomes the hydrodynamic Rossby wave.