Computational and Applied Mathematics: Magnetic fields in stars and planets are generated by a dynamo process that results from multi-scale interactions of the flows in conducting fluids. On the large-scales, these flows are dominated by a strong zonal component, while the magnetic fields exhibit a strong toroidal/zonal character. Although dissi-pation certainly acts on these flows, the kinematic and magnetic viscosities associated with these large-scale flows are small, so that, over the timescale of several years and beyond, the system may be modelled as a conservative one. In this context, the Hamiltonian formulation may give several insights, providing a systematic way to relate symmetries of the system with conservation laws. In the present article, we introduce the Hamiltonian formulation for a model that reasonably describes the dynamics of large-scale flows in stars and planets: the two-dimensional magnetohydrodynamic quasi-geostrophic equations. In this context, we find the invariants of the system, which are of two kinds: the Casimirs, related to the particle relabelling symmetry, and the zonal momentum, which is related to the translational invariance in the zonal direction. We then use these invariants to study the stability of some stationary solutions that are relevant for geophysical and astrophysical applications.
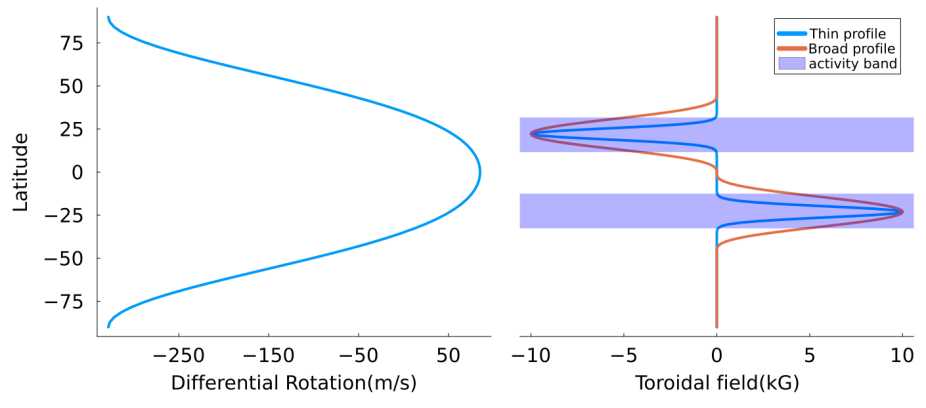
The left panel shows the differential rotation profile at the solar tachocline and the left panel shows different toroidal field profiles. The ratio between the meridional gradient of those quantities is determinant in the stability/instability properties of the tachocline flows.