Appendix
Units and notation for angular measures
It is customary to divide the circle into 360 degrees, and to subdivide each degrees in 60 minutes, and in turn each minute into 60 seconds. If needed, seconds are subdivided in the usual decimal manner. Prime (’)and double-primes (") are used to indicate minutes and seconds, e.g., 30° 20′ 20" means 30 degrees 20 minutes 20 seconds, which is equivalent within a second to to 30 1/3°. Astronomy has inherited this peculiar base-60 system from the ancient Babylonians.
Seasons and the Earth′s orbit
A common misconception is that seasons are caused by a yearly variation of the Earth-Sun distance. If this were so, winter would occur simultaneously in the northern and Southern hemispheres, contrary to direct experience. Despite such an obvious counterproof, this misconception remains widespread.
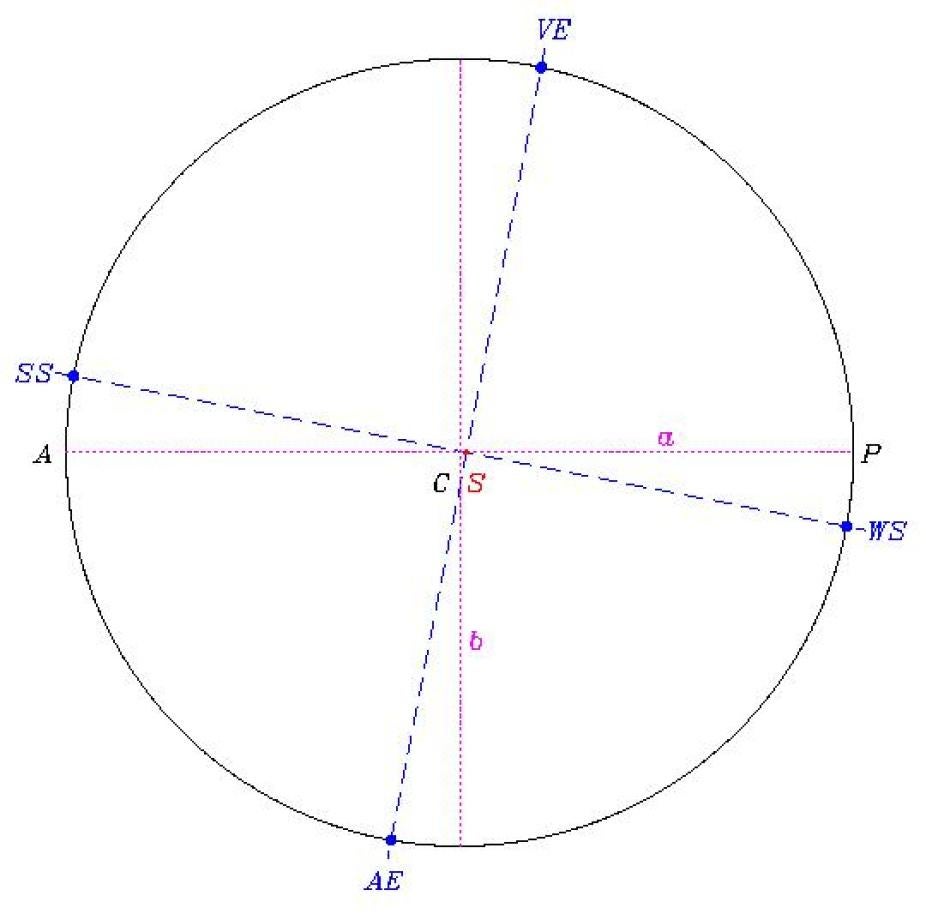
Figure 1. The orbit of the Earth around the Sun (solid line). The orbit is an ellipse of very low eccentricity (e=0.017). The Sun (S), drawn to scale, is the small solid dot at the intersection of the two dashed lines, and is located at a focus of the ellipse, which is offset from the geometrical center of the ellipse (C) by a distance e a, along the major axis of the ellipse (horizontal dotted line). The perihelion is at P, and the aphelion at A. The line segment CP, of length a, is the semi-major axis. The minor axis of the ellipse (vertical dotted line) has a half length b/a=(1-e2)1/2 (=0.99985 here), so that the Earth′s orbit is very nearly circular. The positions along the orbit corresponding to vernal and automnal equinoxes (VE and AE) and winter and summer solstices (WS and SS) are indicated by solid dots; note that the VEAE and WSSS line segments (dashed lines) intersect at 90° by definition, independently of the eccentricity of the orbit.
Figure 1 shows the elliptical shape of the Earth′s orbit around the Sun. The Earth revolves in a counterclockwise sense, as seen from the North ecliptic pole. The Sun, drawn to scale, is the small solid dot located slightly left of the geometrical center of the ellipse, and sits at one focus of the ellipse; this is in fact Kepler′s first Law of planetary motion (the fact that the second focus is empty bothered Kepler quite a bit, for mystico-aesthetic reasons). The perihelion is the point along the orbit of closest approach to the Sun, and the aphelion the opposite point of maximum distance to the Sun. Because the Earth′s orbit is of very low eccentricity, its elliptical shape is very close to a circle. The locations along the orbit of the solstices (winter: WS, summer: SS) and equinoxes (vernal: VE, autumnal: AE) are indicated by solid dots. These are defined entirely in terms of the inclination of the Earth′s orbital axis with respect to the Sun, and thus have no special relationship to the orientation of Earth′s orbit in space. It is because the orbit is so very nearly circular that the seasons have essentially nothing to do with the distance between the Sun and Earth. The Sun-Earth distance varies in fact by 3.4% over the year, and the Earth reaches perihelion on January 2. While a 3.4% distance variation certainly leads to a small variation of the net energy flux to Earth, heat absorption and release by the oceans almost completely damps this variation in the course of one year. Consequently, variations in energy flux due to the varying altitude of the Sun in the sky completely dominate the local variation of net incident solar energy.
Kepler′s second law of planetary motion states that the Sun-Earth radius vector sweeps equal areas in equal time intervals. This means that the Earth moves slightly faster along its orbit near perihelion than near aphelion. This, combined with the fact that the solstitial line SSWS coincides with neither the major or minor axis of the ellipse, means that the number of days between each solstice and following equinox, and each equinox and following solstice, is not constant; it takes 92.75 days to go from VE to SS, 93.625 days from SS to AE, 90.825 days from AE to WS, and 88.0 days from WS to VE.
The Earth′s rotation leads to a slight bulging of its equatorial regions The gravitational pull of the Sun (mostly) on this bulge leads to the precession of the Earth′s orbital axis. Precession does not alter the 23.5° inclination angle between the Earth′s spin and orbital axes; it simply leads to a slow rotation of the orientation of the spin axis in space, in turn producing a slow variation of the equinox and solstices direction with respect to the celestial sphere. On Figure 1, the intersecting dashed lines defining those two directions rotate counterclockwise, undergoing a full revolution in about 26000 years. The horizon azimuths of solstices and equinoxes are not affected by precession. However the number of days between solstices and equinoxes will, so that the days of solstices and equinoxes will vary slightly (in which way these dates will change is determined by calendrical conventions).
The gravitational pull of the other planets in the solar system also leads to a second, much slower variation of the angle between the Earth′s spin and orbital axes (equivalently, of the obliquity of the ecliptic, as it is usually referred to in astronomy textbooks). This does alter the horizon azimuths of solstices and equinoxes, but this motion only amounts to about 10′ in 1000 years, which at 36° latitude translates to a bit less than 1/3 of the solar diameter on the horizon. This is small enough to be neglected in our discussions of horizon calendars and window alignments.
Azimuth-altitude coordinates
The intersection of a plane tangent to the Earth′s surface at the observer′s location with the celestial sphere defines the observer′s horizon, which is divided in four equal intervals by the North-South (NS) and East-West (EW) lines. The point Z directly overhead is the zenith, and only half of the celestial sphere is visible from O at any given time. As a consequence of the Earth′s daily rotation, the celestial sphere appears to undergo a full revolution in 24 hours.
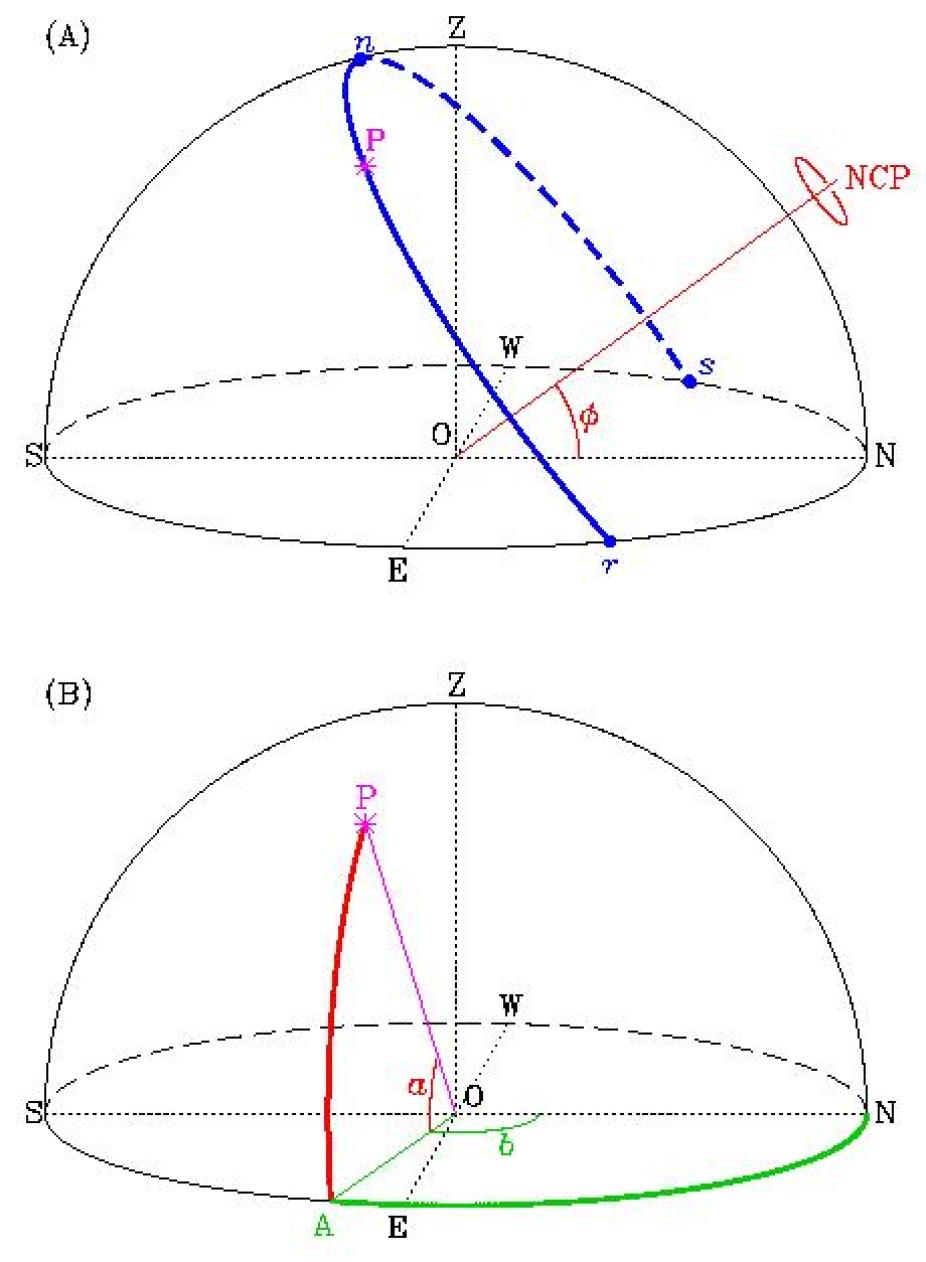
Figure 2. The celestial sphere and astronomical observations. (A) Apparent daily path of an astronomical object P caused by Earth′s rotation. The apparent axis of rotation passes through the observer′s location O on the Earth′s surface, and points to the North Celestial Pole (NCP). The object P rises in the Eastern hemisphere at r and sets in the western hemisphere at s. The diagram is drawn for an observed located at a latitude of 36°, a good representative value for the ancient Anasazi world. (B) The azimuth-altitude coordinate system, defined locally in terms of the observer′s position on the Earth′s surface. Altitude is measured upwards from the observer′s horizon plane, and azimuth clockwise (seen from the zenith Z) from North. Note that the daily motion involves changes in both azimuth and altitude, and that the altitude of the NCP is equal to the observer′s latitude Φ.
Figure 2 illustrates the basic geometry of "fixed-Earth" celestial observation. Consider an observer standing on Earth′s surface at O, looking at a celestial object located at a point P on the celestial sphere.For the observer at O, the apparent axis of rotation lies in the direction of the North Celestial Pole (NCP on Figure 2 [A]). The azimuth of the NCP (=0°) is in fact what defines the direction "North". The altitude of the NCP is equal to the observer′s geocentric latitude Φ. Figure 2 (A) is drawn for Φ=36°, corresponding to Chaco Canyon, New Mexico. The thick line indicate the direction of P′s apparent daily motion, which is opposite to the Earth′s spin direction. Unless P lies within an angular distance Φ of the NCP, its daily path will intersect the horizon at two points r and s, which respectively define its rising and setting azimuth. P moves at constant (angular) speed along its daily path, covering 15° in one hour.
Two quantities are needed to define P′s position on the celestial sphere. Consider on Figure 2 (B) a vertical plane defined by the points O, P and Z; this plane intersects the tangent plane along a line segment OA, where A is the point of intersection with the horizon. The altitude, measured from the horizon, is the angle a=POA corresponding to the angular distance between OA and the observer′s line-of-sight OP (0 ≤ a ≤ 90°). The azimuth is the angle b=NOA corresponding to the angular position of A measured from a reference direction taken conventionally to be North (0 ≤ b ≤ 360°). The East, South and West cardinal direction have azimuth 90°, 180°, and 270° respectively. Evidently, daily rotation of the Earth will affect both the azimuth and altitude of P; its altitude is zero at r and s, and is maximal at n, corresponding to an azimuth of 180° (due South), If P is the Sun, then n defines local solar noon.
Measuring the Sun′s altitude is in principle possible with a gnomon, which is nothing more than a long stick set vertically in the ground. The slow rotation and lengthening or shortening of the stick′s shadow reflects the Sun′s changes in azimuth and altitude. This is the basic operational principle behind Sun dials. The progression of the seasons can then be followed by tracking the day-to-day variations in length of the gnomon′s shadow at solar noon, occurring when the shadow is the shortest on a given day. To do so accurately requires that the stick be placed vertically, which is straightforward to do with a plumb line, and that the surface on which the shadow is projected is perfectly flat and exactly horizontal. which is much harder.